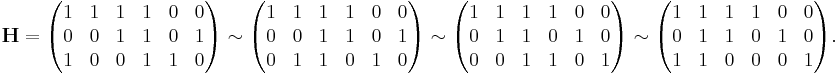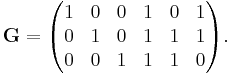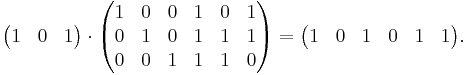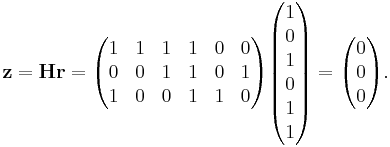Low-density parity-check code

In information theory, a low-density parity-check (LDPC) code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel,[1][2] and is constructed using a sparse bipartite graph.[3] LDPC codes are capacity-approaching codes, which means that practical constructions exist that allow the noise threshold to be set very close (or even arbitrarily close on the BEC) to the theoretical maximum (the Shannon limit) for a symmetric memory-less channel. The noise threshold defines an upper bound for the channel noise, up to which the probability of lost information can be made as small as desired. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length.

LDPC codes are finding increasing use in applications where reliable and highly efficient information transfer over bandwidth or return-channel constrained links in the presence of data-corrupting noise is desired. Although implementation of LDPC codes has lagged behind that of other codes, notably turbo codes, the absence of encumbering software patents has made LDPC attractive to some.[4]

LDPC codes are also known as Gallager codes, in honor of Robert G. Gallager, who developed the LDPC concept in his doctoral dissertation at MIT in 1960.[5]

Contents

History

Impractical to implement when first developed by Gallager in 1963,[6] Gallager's LDPC codes were forgotten until Gallager's work was discovered in 1996.[7] Turbo codes, another class of capacity-approaching codes discovered in 1993, became the coding scheme of choice in the late 1990s, used for applications such as deep space satellite communications. However, in the last few years, the advances in low-density parity-check codes have seen them surpass turbo codes in terms of error floor and performance in the higher code rate range, leaving turbo codes better suited for the lower code rates only.[8]

Applications

In 2003, an LDPC code beat six turbo codes to become the error correcting code in the new DVB-S2 standard for the satellite transmission of digital television.[9] In 2008, LDPC beat convolutional turbo codes as the FEC scheme for the ITU-T G.hn standard.[10] G.hn chose LDPC over turbo codes because of its lower decoding complexity (especially when operating at data rates close to 1 Gbit/s) and because the proposed turbo codes exhibited a significant error floor at the desired range of operation.[11] LDPC is also used for 10GBase-T Ethernet, which sends data at 10 gigabits per second over twisted-pair cables. As of 2009, LDPC codes are also part of the Wi-Fi 802.11 standard as an optional part of 802.11n, in the High Throughput (HT) PHY specification [12].

Function

LDPC codes are defined by a sparse parity-check matrix. This sparse matrix is often randomly generated, subject to the sparsity constraints. These codes were first designed by Gallager in 1962.

Below is a graph fragment of an example LDPC code using Forney's factor graph notation. In this graph, n variable nodes in the top of the graph are connected to (n−k) constraint nodes in the bottom of the graph. This is a popular way of graphically representing an (n, k) LDPC code. The bits of a valid message, when placed on the T's at the top of the graph, satisfy the graphical constraints. Specifically, all lines connecting to a variable node (box with an '=' sign) have the same value, and all values connecting to a factor node (box with a '+' sign) must sum, modulo two, to zero (in other words, they must sum to an even number).

Ignoring any lines going out of the picture, there are 8 possible 6-bit strings corresponding to valid codewords: (i.e., 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111). This LDPC code fragment represents a 3-bit message encoded as six bits. Redundancy is used, here, to increase the chance of recovering from channel errors. This is a (6, 3) linear code, with n = 6 and k = 3.

Once again ignoring lines going out of the picture, the parity-check matrix representing this graph fragment is

\mathbf{H} = \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ \end{pmatrix}.

In this matrix, each row represents one of the three parity-check constraints, while each column represents one of the six bits in the received codeword.

In this example, the eight codewords can be obtained by putting the parity-check matrix H into this form 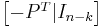\begin{bmatrix} -P^T | I_{n-k} \end{bmatrix} through basic row operations:

\mathbf{H} = \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ \end{pmatrix} \sim \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ \end{pmatrix} \sim \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ \end{pmatrix} \sim \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \\ \end{pmatrix}.

From this, the generator matrix G can be obtained as 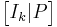\begin{bmatrix} I_k | P \end{bmatrix} (noting that in the special case of this being a binary code 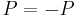P = -P), or specifically:

\mathbf{G} = \begin{pmatrix} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 0 \\ \end{pmatrix}.

Finally, by multiplying all eight possible 3-bit strings by G, all eight valid codewords are obtained. For example, the codeword for the bit-string '101' is obtained by:

\begin{pmatrix} 1 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 0 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 1 & 0 & 1 & 1 \\ \end{pmatrix}.

Decoding

As with other codes, optimally decoding an LDPC code on the binary symmetric channel is an NP-complete problem, although techniques based on iterative belief propagation used in practice lead to good approximations. In contrast, belief propagation on the binary erasure channel is particularly simple where it consists of iterative constraint satisfaction.

For example, consider that the valid codeword, 101011, from the example above, is transmitted across a binary erasure channel and received with the first and fourth bit erased to yield ?01?11. Since the transmitted message must have satisfied the code constraints, the message can be represented by writing the received message on the top of the factor graph.

In this example, the first bit cannot yet be recovered, because all of the constraints connected to it have more than one unknown bit. In order to proceed with decoding the message, constraints connecting to only one of the erased bits must be identified. In this example, either the second or third constraint suffices. Examining the second constraint, the fourth bit must have been 0, since only a 0 in that position would satisfy the constraint.

This procedure is then iterated. The new value for the fourth bit can now be used in conjunction with the first constraint to recover the first bit as seen below. This means that the first bit must be a 1 to satisfy the leftmost constraint.

Thus, the message can be decoded iteratively. For other channel models, the messages passed between the variable nodes and check nodes are real numbers, which express probabilities and likelihoods of belief.

This result can be validated by multiplying the corrected codeword r by the parity-check matrix H:

\mathbf{z} = \mathbf{Hr} = \begin{pmatrix} 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ \end{pmatrix}.

Because the outcome z (the syndrome) of this operation is the 3 × 1 zero vector, the resulting codeword r is successfully validated.

Updating node information

In recent years, there has also been a great deal of work spent studying the effects of alternative schedules for variable- and constraint-node update. The original technique that was used for decoding LDPC codes was known as flooding. This type of update required that, before updating a variable node, all constraint nodes needed to be updated and vice versa. In later work by Vila Casado et al.,[13] alternative update techniques were studied, in which variable nodes are updated with the newest available check-node information.

The intuition behind these algorithms is that variable nodes whose values vary the most are the ones that need to be updated first. Highly reliable nodes, whose log-likelihood ratio (LLR) magnitude is large and does not change significantly from one update to the next, do not require updates with the same frequency as other nodes, whose sign and magnitude fluctuate more widely. These scheduling algorithms show greater speed of convergence and lower error floors than those that use flooding. These lower error floors are achieved by the ability of the Informed Dynamic Scheduling (IDS)[13] algorithm to overcome trapping sets of near codewords.[14]

When non-flooding scheduling algorithms are used, an alternative definition of iteration is used. For an (n, k) LDPC code of rate k/n, a full iteration occurs when n variable and n − k constraint nodes have been updated, no matter the order in which they were updated.

Code construction

For large block sizes, LDPC codes are commonly constructed by first studying the behaviour of decoders. As the block size tends to infinity, LDPC decoders can be shown to have a noise threshold below which decoding is reliably achieved, and above which decoding is not achieved.[15] This threshold can be optimised by finding the best proportion of arcs from check nodes and arcs from variable nodes. An approximate graphical approach to visualising this threshold is an EXIT chart.

The construction of a specific LDPC code after this optimisation falls into two main types of techniques:

Construction by a pseudo-random approach builds on theoretical results that, for large block size, a random construction gives good decoding performance.[7] In general, pseudo-random codes have complex encoders, however pseudo-random codes with the best decoders can have simple encoders.[16] Various constraints are often applied to help ensure that the desired properties expected at the theoretical limit of infinite block size occur at a finite block size.

Combinatorial approaches can be used to optimise properties of small block-size LDPC codes or to create codes with simple encoders.

Yet another way of constructing LDPC codes is to use finite geometries. This method was proposed by Y. Kou et al. in 2001.[17]

See also

People

Theory

Applications

Other capacity-approaching codes

References

  1. ^ David J.C. MacKay (2003) Information theory, Inference and Learning Algorithms, CUP, ISBN 0-521-64298-1, (also available online)
  2. ^ Todd K. Moon (2005) Error Correction Coding, Mathematical Methods and Algorithms. Wiley, ISBN 0-471-64800-0 (Includes code)
  3. ^ Amin Shokrollahi (2003) LDPC Codes: An Introduction
  4. ^ NewScientist, Communication speed nears terminal velocity, by Dana Mackenzie, 9 July 2005
  5. ^ Larry Hardesty (21 January 2010), "Explained: Gallager codes", MIT News, http://web.mit.edu/newsoffice/2010/gallager-codes-0121.html, retrieved 2010-08-18 
  6. ^ Gallager, R. G., Low Density Parity Check Codes, Monograph, M.I.T. Press, 1963 [1]
  7. ^ a b David J.C. MacKay and Radford M. Neal, "Near Shannon Limit Performance of Low Density Parity Check Codes," Electronics Letters, July 1996
  8. ^ Telemetry Data Decoding, Design Handbook
  9. ^ Presentation by Hughes Systems
  10. ^ HomePNA Blog: G.hn, a PHY For All Seasons
  11. ^ IEEE Communications Magazine paper on G.hn
  12. ^ IEEE Standard, section 20.3.11.6 "802.11n-2009", IEEE, October 29, 2009, accessed March 21, 2011.
  13. ^ a b A.I. Vila Casado, M. Griot, and R.Wesel, “Informed dynamic scheduling for belief propagation decoding of LDPC codes,” Proc. IEEE Int. Conf. on Comm. (ICC), June 2007.
  14. ^ T. Richardson, “Error floors of LDPC codes,” in Proc. 41st Allerton Conf. Comm., Control, and Comput., Monticello, IL, 2003.
  15. ^ Thomas J. Richardson and M. Amin Shokrollahi and Rüdiger L. Urbanke, "Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes," IEEE Transactions in Information Theory, 47(2), February 2001
  16. ^ Thomas J. Richardson and Rüdiger L. Urbanke, "Efficient Encoding of Low-Density Parity-Check Codes," IEEE Transactions in Information Theory, 47(2), February 2001
  17. ^ Y. Kou, S. Lin and M. Fossorier, "Low-Density Parity-Check Codes Based on Finite Geometries: A Rediscovery and New Results," IEEE Transactions on Information Theory, vol. 47, no. 7, November 2001, pp. 2711- 2736.
  18. ^ http://spectrum.ieee.org/consumer-electronics/standards/does-china-have-the-best-digital-television-standard-on-the-planet/2

External links